Basic Ray-Tracing Algorithm
Light Rays
Three ideas about light rays
- Light travels in straight lines (though this is wrong)
- Light rays do not “collide” with each other if they cross (though this is still wrong)
- Light rays travel from the light sources to the eye (but the physics is invariant under path reversal - reciprocity).
Ray Casting
Appel 1968 - Ray casting
- Generate an image by casting one ray per pixel
- Check for shadows by sending a ray to the light
Ray Casting - Generating Eye Rays
Shading Pixels (Local Only)
Pinhole Camera Model
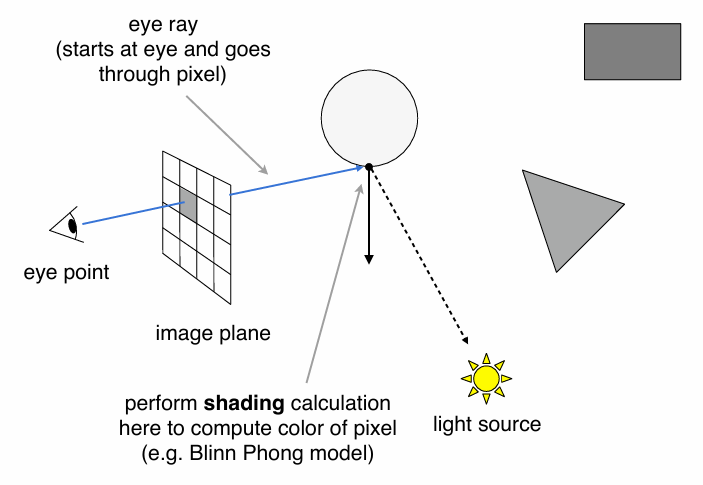
每个像素投射出一条光线,求与物体相交最近的点,将该点用于计算光照着色
Recursive (Whitted-Style) Ray Tracing
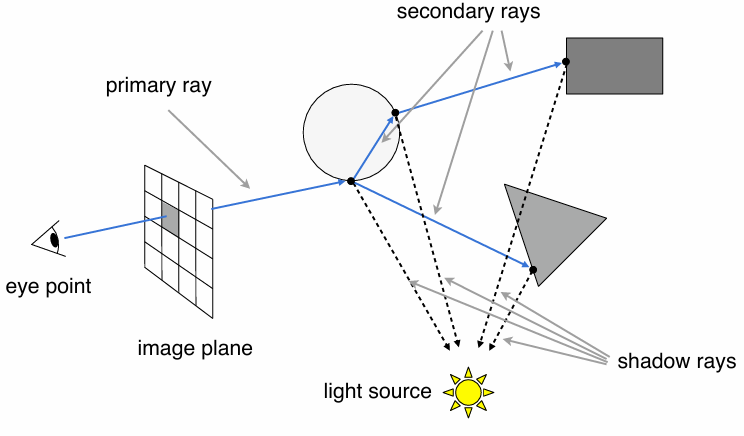
每个像素投射出一条光线,在物体上进行折射和反射,然后计算折射和反射后光线与物体的所有交点,
然后计算每个交点的光照着色,再根据一个权重加到像素颜色上
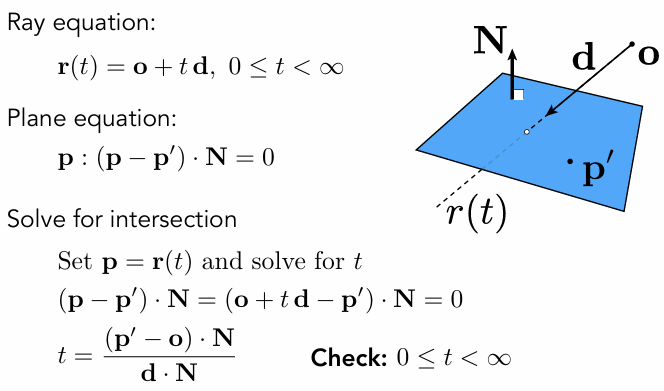
Ray-Surface Intersection
Ray Equation
Ray is defined by its origin and a direction vector
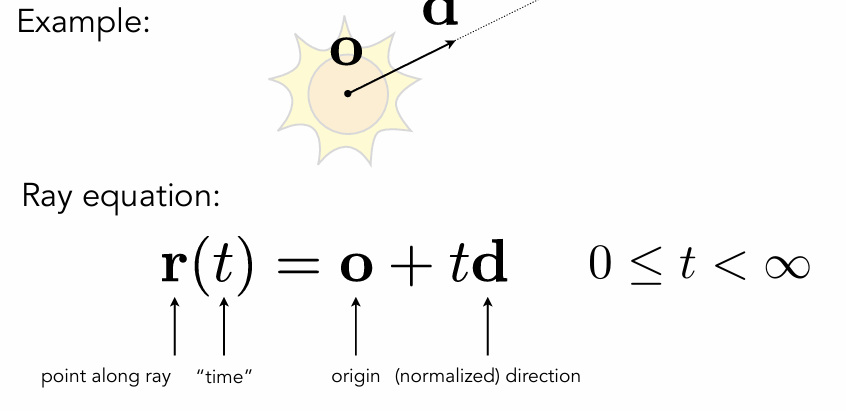 、
、
Ray Intersection With Sphere
相交点满足光线和圆的两个方程
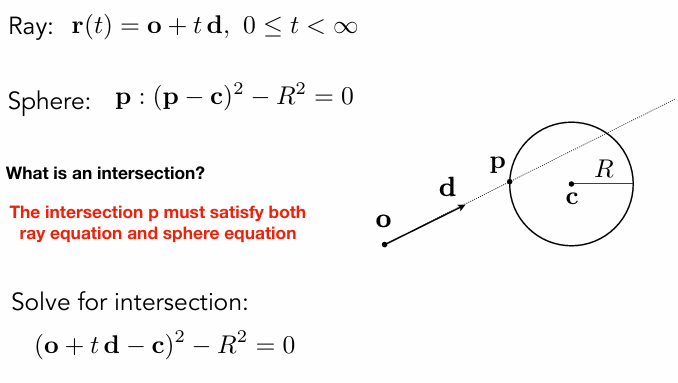

Ray Intersection With Implicit Surface

需要t大于等于0 且解是实数
Ray Intersection With Triangle Mesh
Triangle is in a plane
• Ray-plane intersection
• Test if hit point is inside triangle
Many ways to optimize…
先判断和平面是否相交,再判断交点是否在三角形内、
Plane Equation

Ray Intersection With Plane
下面有更简单的方法,直接求出光线和三角形的交点
Möller Trumbore Algorithm
A faster approach, giving barycentric coordinate directly Derivation in the discussion section!
用重心坐标来描述三角形内的点(公式右边)
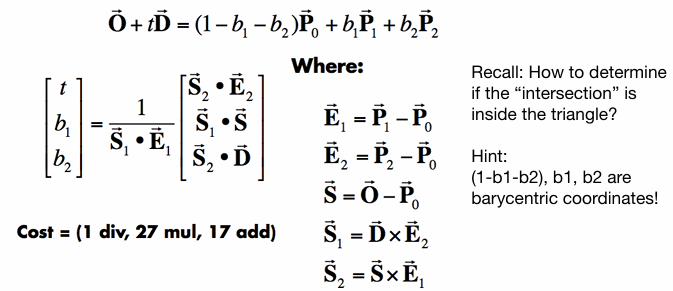
解出来后需要判断 t非负且重心坐标三个坐标非负
Accelerating Ray-Surface Intersection
Ray Tracing – Performance Challenges
Simple ray-scene intersection
• Exhaustively test ray-intersection with every triangle
• Find the closest hit (i.e. minimum t)
Problem:
• Naive algorithm = #pixels ⨉ # traingles (⨉ #bounces)
• Very slow!
For generality, we use the term objects instead of triangles later (but doesn’t necessarily mean entire objects)
Bounding Volumes 包围盒
Quick way to avoid intersections: bound complex object with a simple volume
• Object is fully contained in the volume
• If it doesn’t hit the volume, it doesn’t hit the object
• So test BVol first, then test object if it hits

Ray-Intersection With Box
Understanding: box is the intersection of 3 pairs of slabs(3个对面)
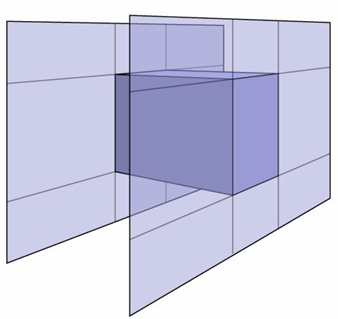
Specifically:
We often use an Axis-Aligned Bounding Box (AABB) (轴对⻬包围盒)
i.e. any side of the BB is along either x, y, or z axis
Ray Intersection with Axis-Aligned Box
2D example; 3D is the same!
Compute intersections with slabs and take intersection of t_min/t_max intervals
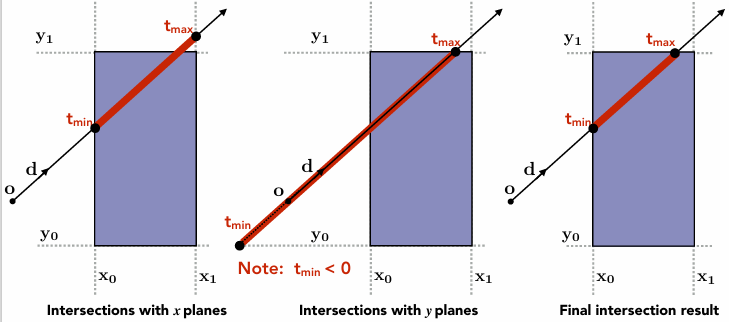
计算t的交集
从3D角度看:
• Recall: a box (3D) = three pairs of infinitely large slabs
• Key ideas
-The ray enters the box only when it enters all pairs of slabs
-The ray exits the box as long as itexitsany pair of slabs
具体计算方法:
For each pair, calculate the tmin and tmax (negative is fine)
For the 3D box, t_enter = max{t_min}, t_exit = min{t_max}
If t_enter < t_exit, we know the ray stays a while in the box (so they must intersect!)
• However, ray is not a line
-Should check whether t is negative for physical correctness!
• What if t_exit < 0?
-The box is “behind” the ray — no intersection!
• What if t_exit >= 0 and t_enter < 0?
-The ray’s origin is inside the box — have intersection!
• In summary, ray and AABB intersect iff (iff指的是当且仅当)
-t_enter < t_exit && t_exit >= 0 最终判断条件
Why Axis-Aligned?
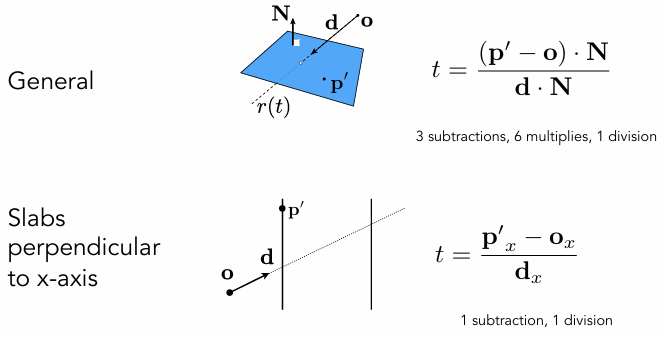
计算简单很多,只需要差值除以对应分量