Shading 3
Barycenric Coordinates 重心坐标
Interpolation Across Triangles 在三角形内部插值
原因:
指定顶点的值后能够获得三角形内部的平滑的变化值
Specify values at vertices
Obtain smoothly varying values across triangles
可以用于:
Texture coordinates, colors, normal vectors, …
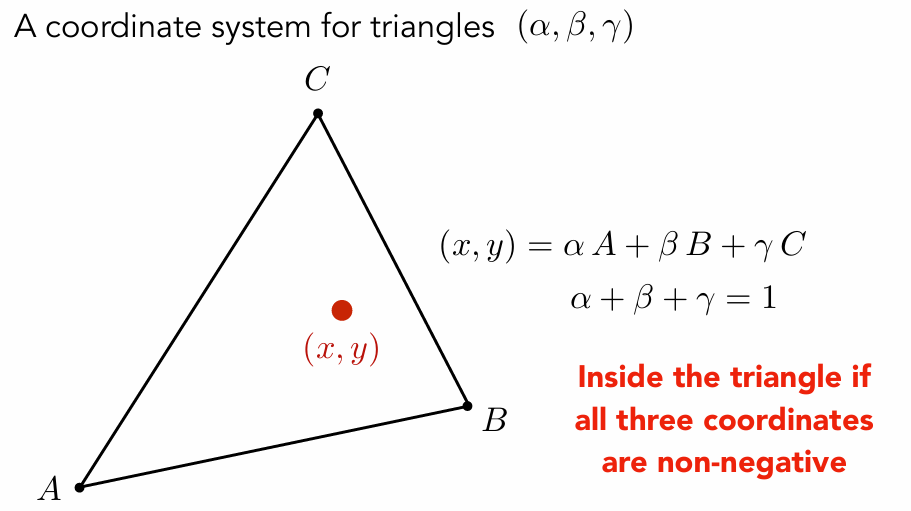
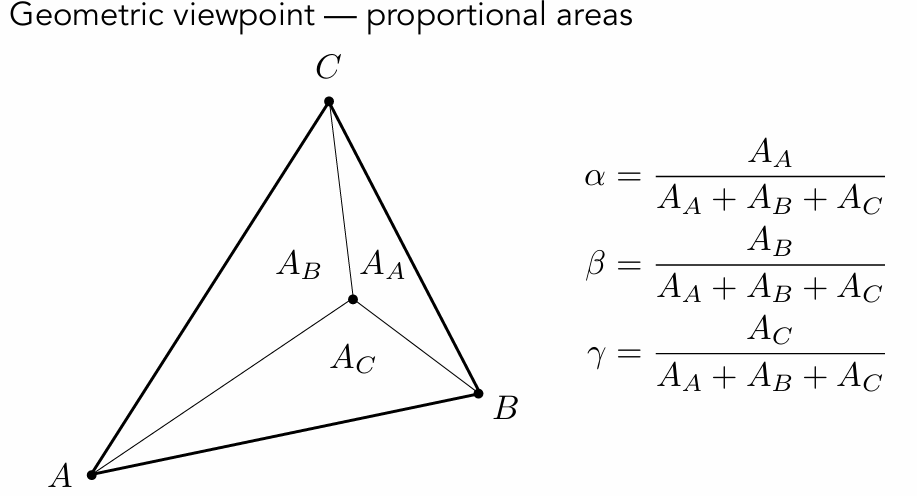
面积又可以用叉积进行计算 S=1/2 || aXb ||
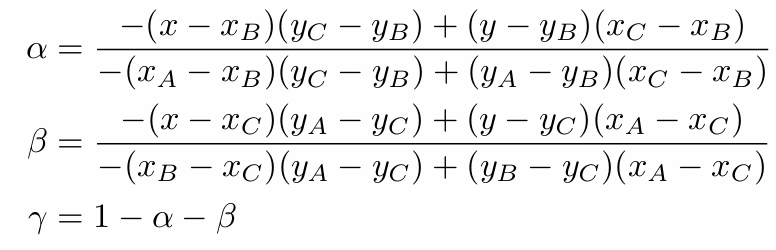
问题:
做投影变换时,重心坐标会发生发生变化。
所以三维空间中的属性需要在三维空间进行插值后,再投影变换到二维空间中去。
Applying texture

认为纹理值是漫反射系数
会出现的问题:Texture Magnification 纹理放大
Generally don’t want this — insufficient texture resolution 纹理分辨率不足
A pixel on a texture — a texel (纹理元素、纹素)

Nearest:一定pixel范围内使用相同的texel
Bilinear:双线性插值

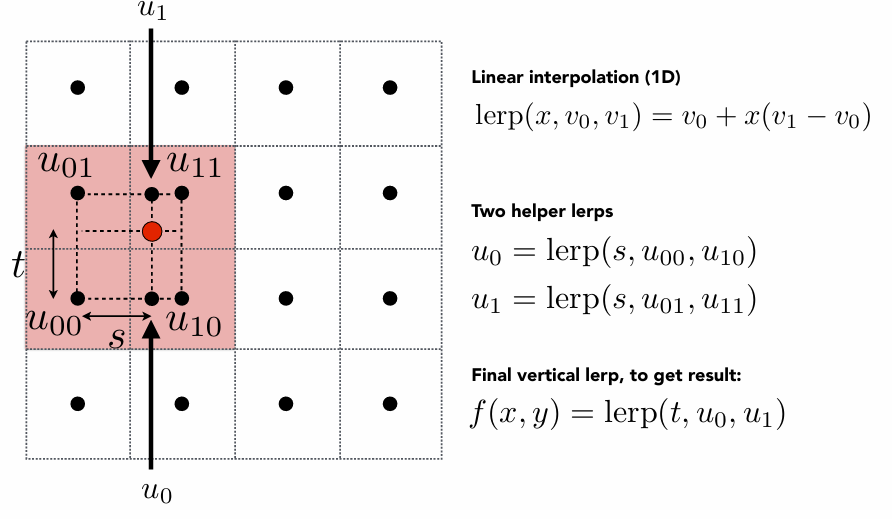
Bicubic:取周围16个点来进行插值。
问题2:纹理缩小 Texture minification(hard case)
会产生走样
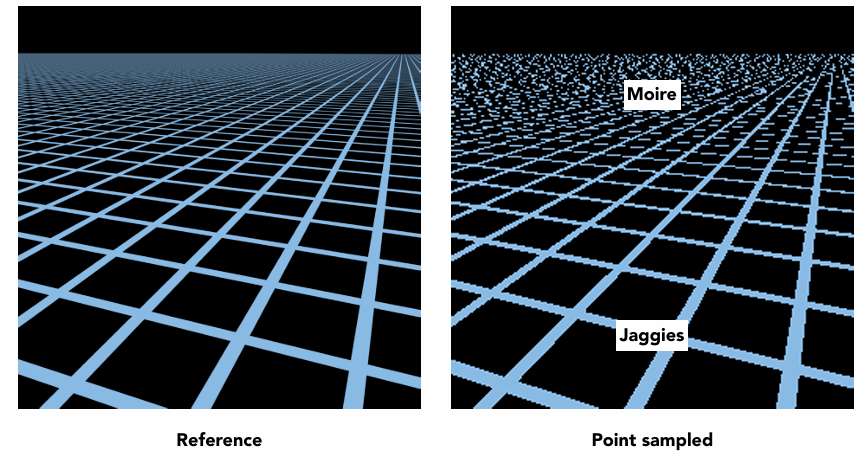
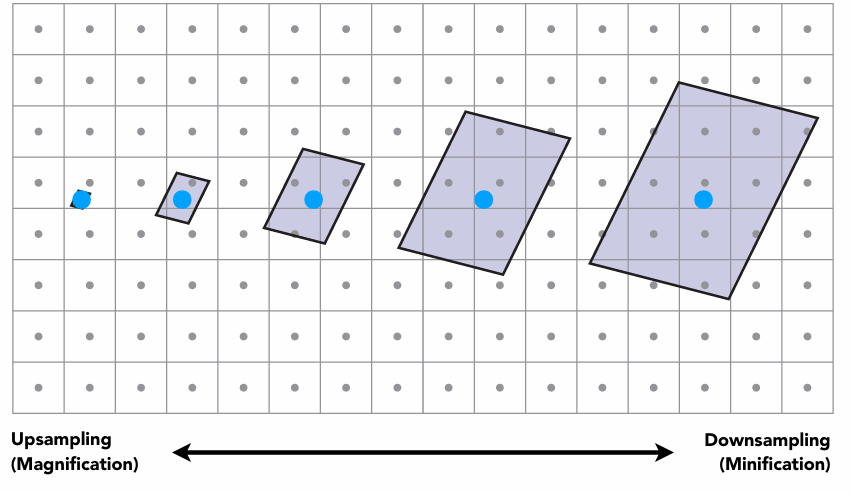
超采样可以解决问题,但是会消耗很多算力
一个像素的信号频率太高
更好的方法(范围查询):
避免采样,直接获取一定区域的平均值
Point Query vs. (Avg.) Range Query
Mipmap:allowing (fast, approx., square) range queries

也叫Mip hierarchy
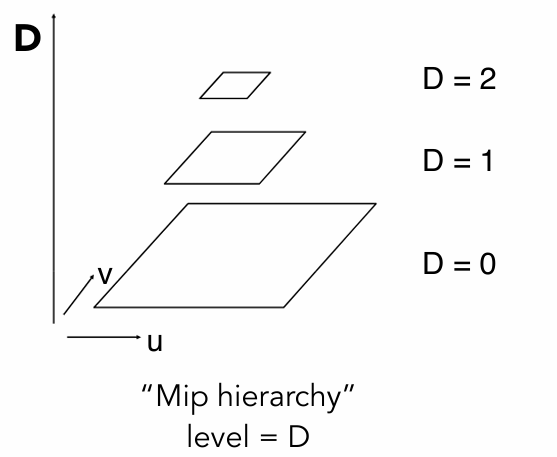
存储开销:
只多了1/3的存储量(每级缩小1/4)
计算Mipmap的Level D:
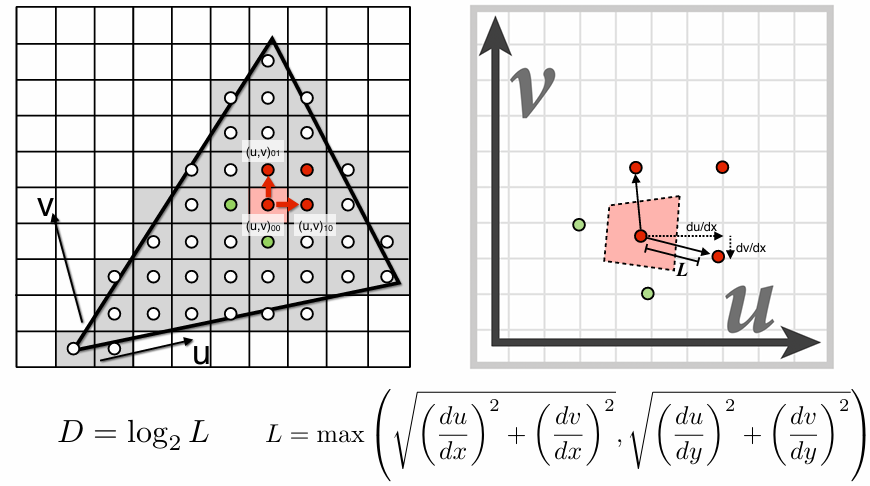
查询1.8层,在两层间进行一次插值。也就是三线性插值
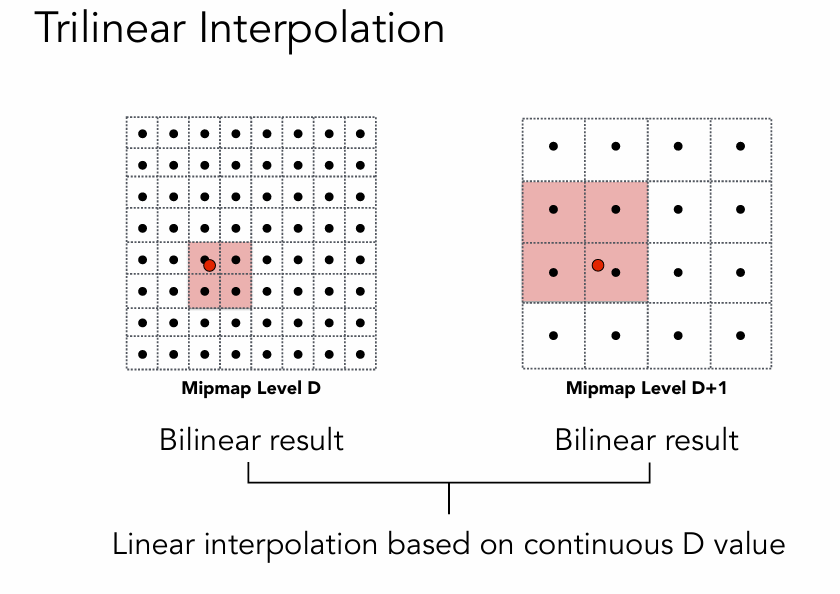
Mipmap的缺陷:
在远处会出现过度模糊。此处主要因为不满足square,不是方形区域的缩小
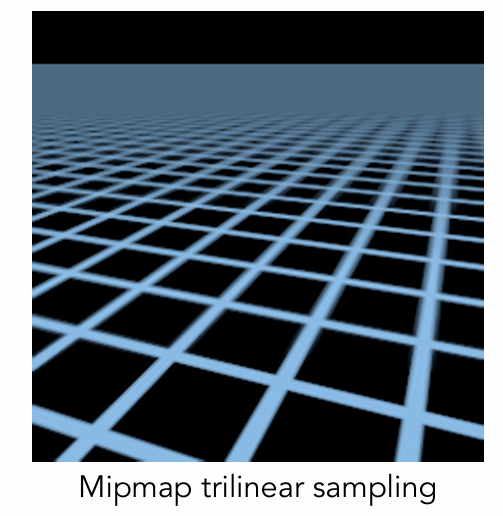
Anisotropic Filtering 各向异性过滤:

存储开销:3倍
各向异性多少x(例如2x,4x,16x)代表了这里的图片压缩多少次,如2x,压缩一次,取左上2x2区域内4个图,4x就是压缩3次,3x3区域内9个图。
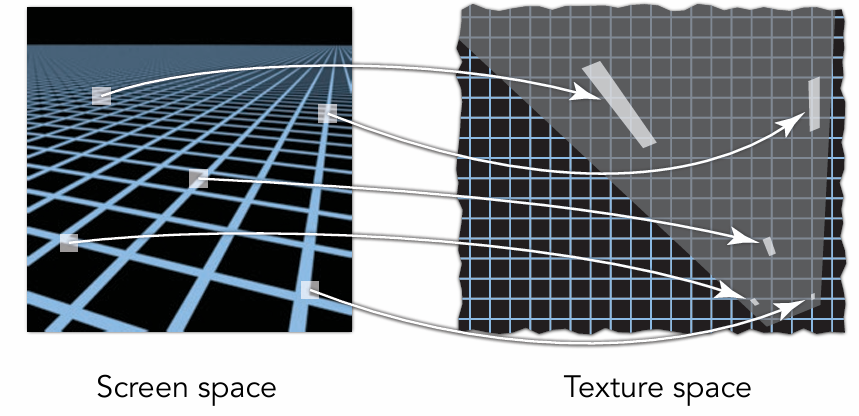
Can look up axis-aligned rectangular zones
Diagonal footprints still a problem
可部分解决该问题,相当于使用矩形,而不只是正方形来获取平均值。但是对于倾斜的区域还是不太好用,如下图最左上角的区域。
质量更好的方法:
EWA filtering
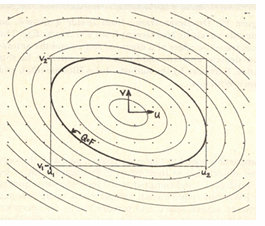
EWA使用多个区域来取平均。但是存储开销更大。