games101-note-L4 Transformation Cont.

3D transformation

1.3D homogeneous coordinates:

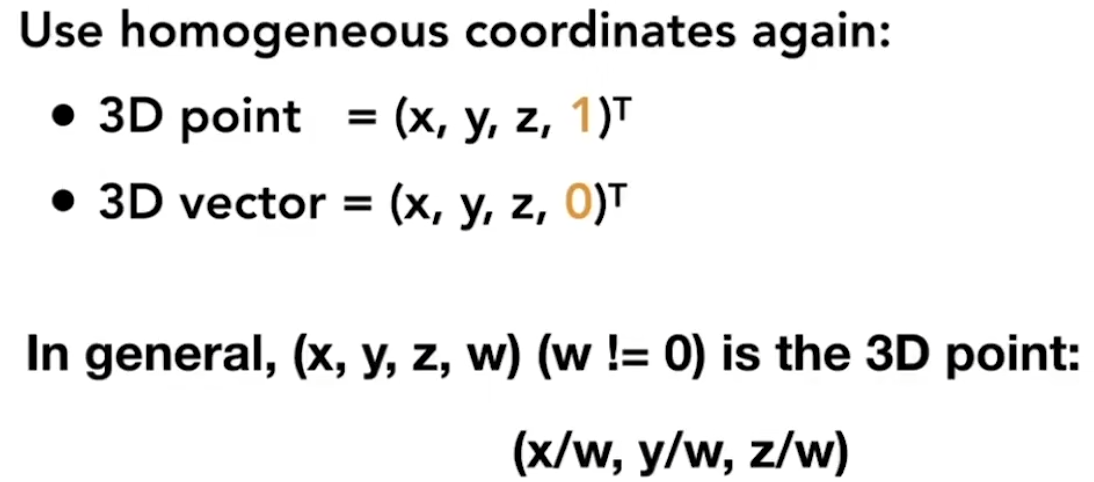
2.3D affine transformations:

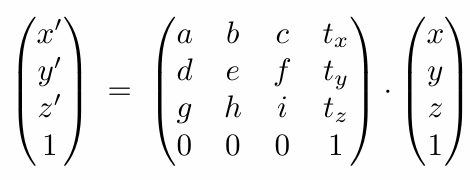
问题：对于仿射变换而言，是先进行平移还是线性变换？

展开后可以得到，是先应用的线性变换，再加上的平移量

3.Rotation around x y z -axis

为什么R_y的sin的符号不一样？

因为应该按照右手螺旋定则 应该是zx -》+ y，所以xz是相反的-y

4.Rodrigues’ Rotation Formula

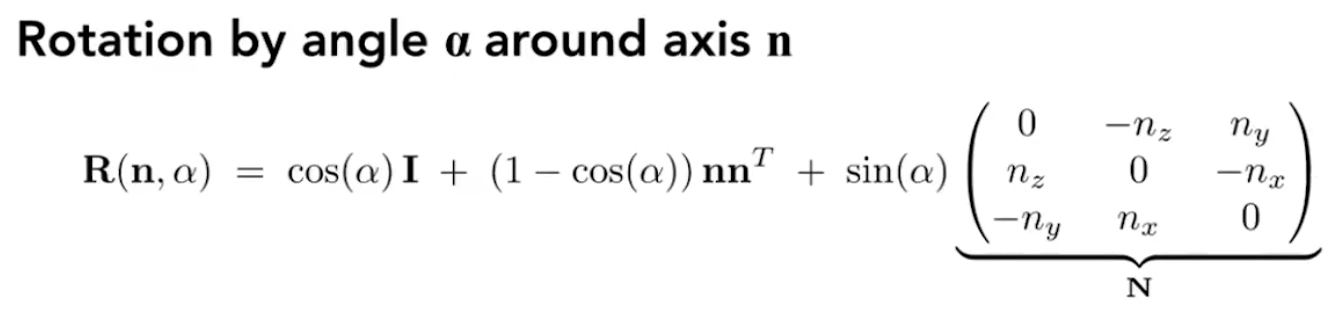
View/Camera Transformation

定义一个相机：

1. 位置
2. 视线方向
3. 向上方向

关键点：当相机和物体一起移动，相片不变
约定：

1.移动相机到The origin, up at Y, look at -Z
2.同时让物体进行相同的移动

因为要先平移再旋转，所以不能直接用仿射变换写出来，要两个单独写再相乘。

Projection transfomsation

1. Orthographic projection

   Translate (center to origin) first, then scale (length/width/height to 2)

   

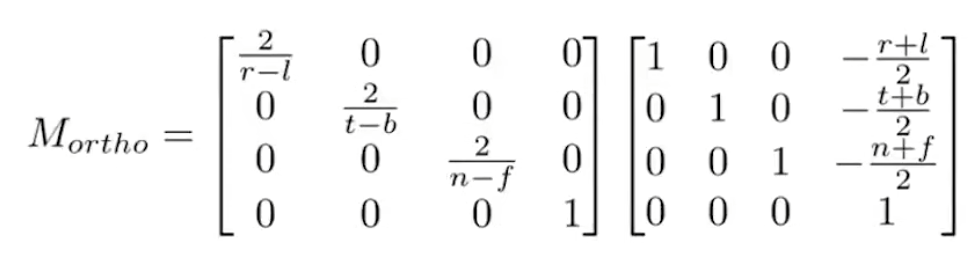
   摄像头沿着-z看，所以n>f。

   所以OpenGL使用了左手坐标系，来让n<f。

2. Perspective projection

   先从透视到正交 M_persp->ortho，再做正交投影 M_ortho
   推导 M_persp->ortho:

   想象将furstum挤压为cuboid

   
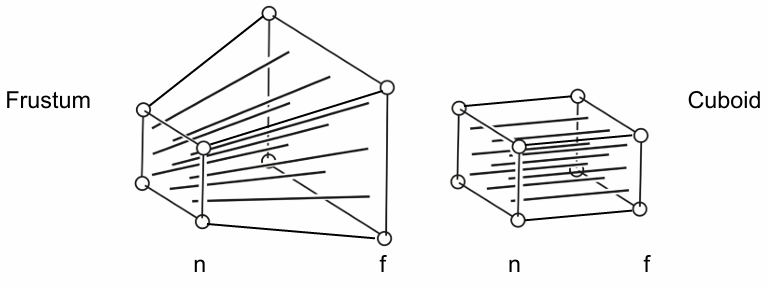
   约定：near面和far面都不变，即z不会变化。并且中心点不会发生变化。

   1. 先用所有同一个面的x, y和near plane满足相似关系，推导出x，y的变换。

      

      
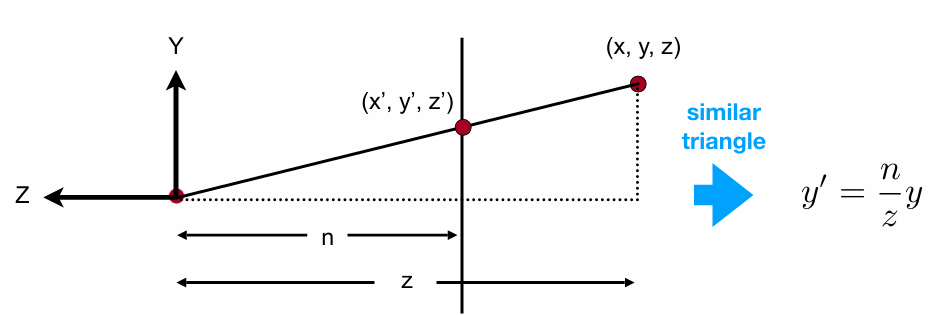
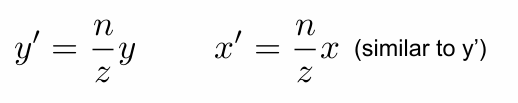
      得到变换前后关系：（广义坐标homogeneous coordinates）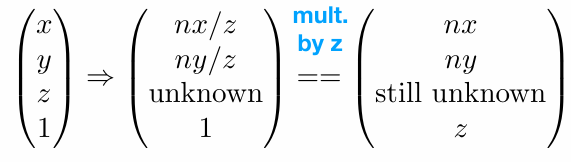

      
      由此推导出变换矩阵的大部分参数：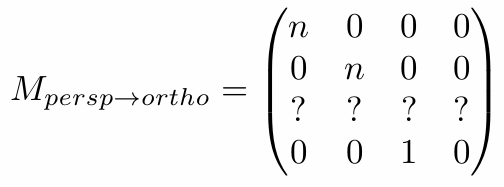

      

   2. 再用near plane需要所有点不变以及far plane的z坐标不变（特别是far plane的中心点完全不变），推导出z的变换。

      Any point on the near plane will not change
      

      So the third row must be of the form (0 0 A B)
      

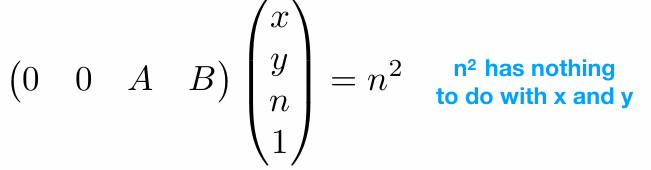
      Any point’s z on the far plane will not change
      

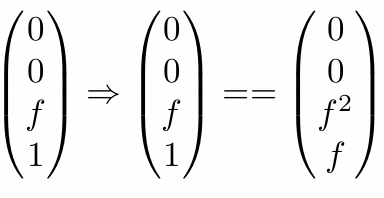
      两个方程，两个未知数，可解出A和B的值:
      
      透视投影矩阵 = 正交投影矩阵 * 透视到正交矩阵