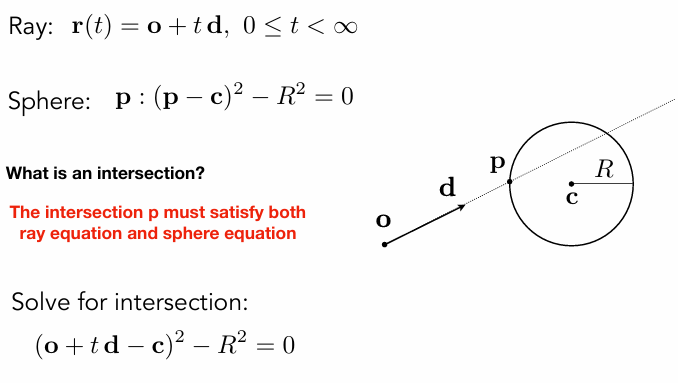
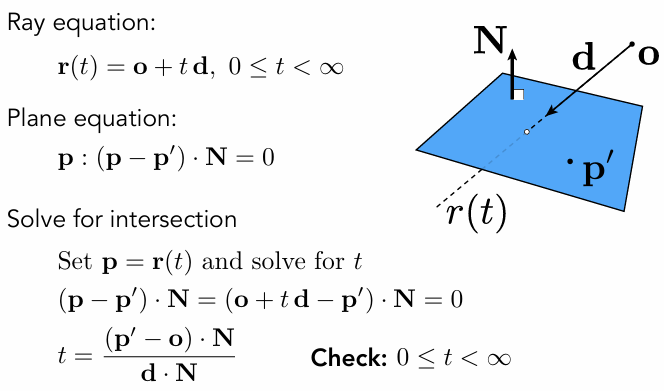
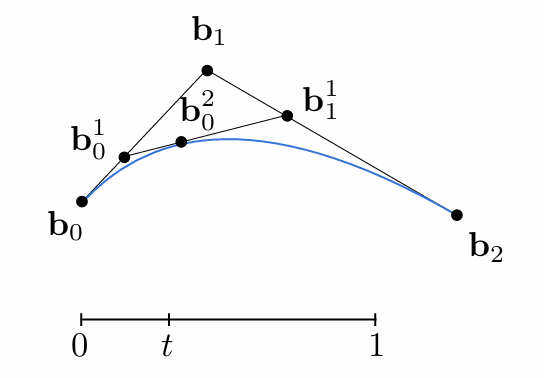
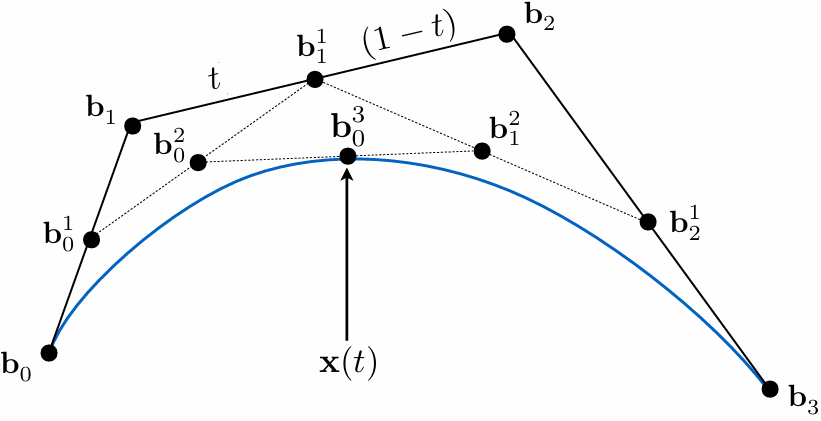
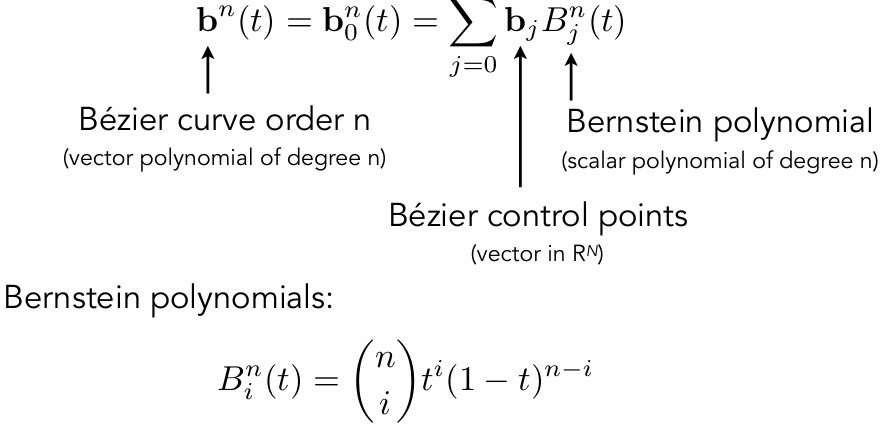
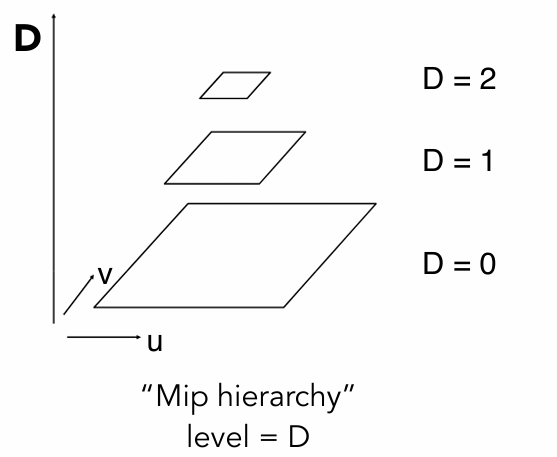
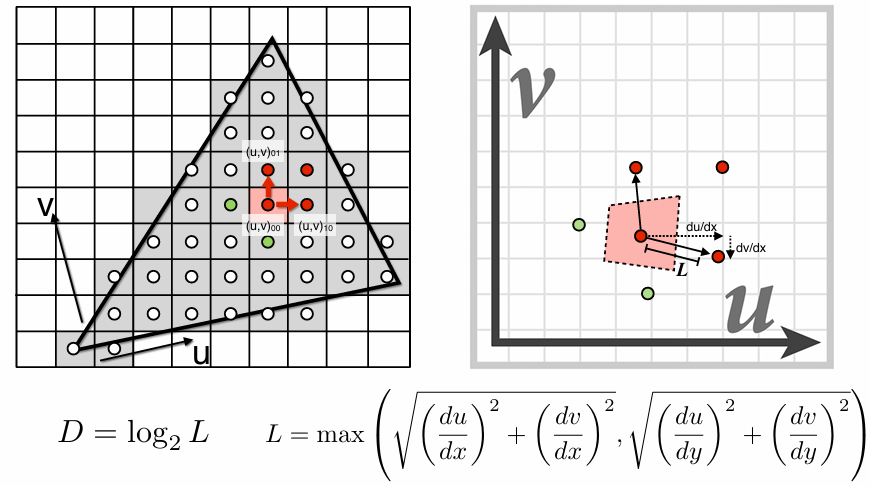
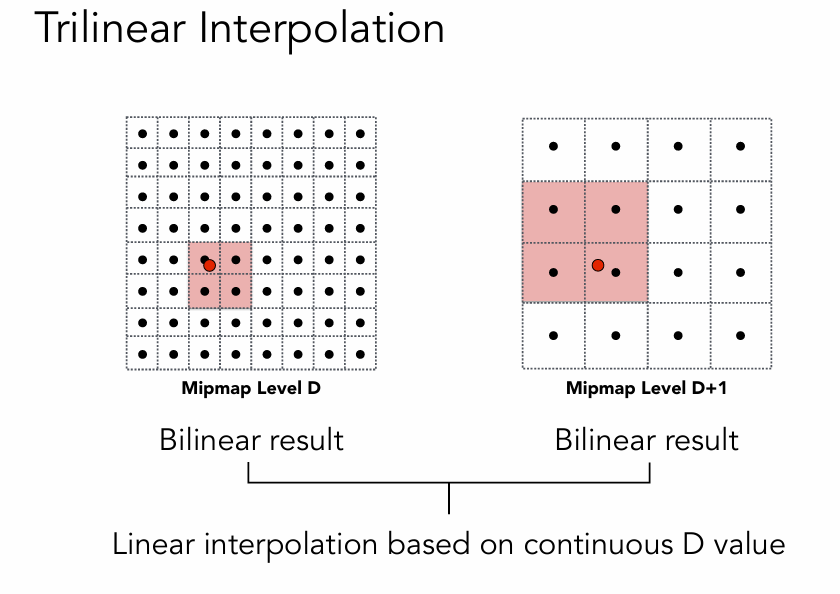
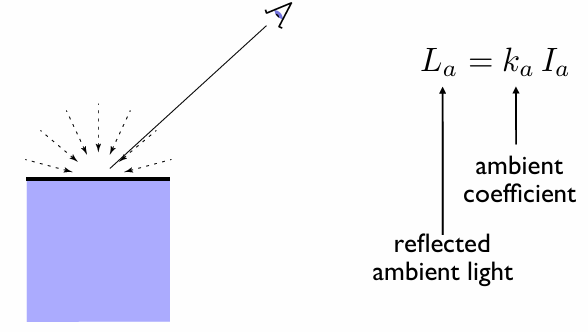
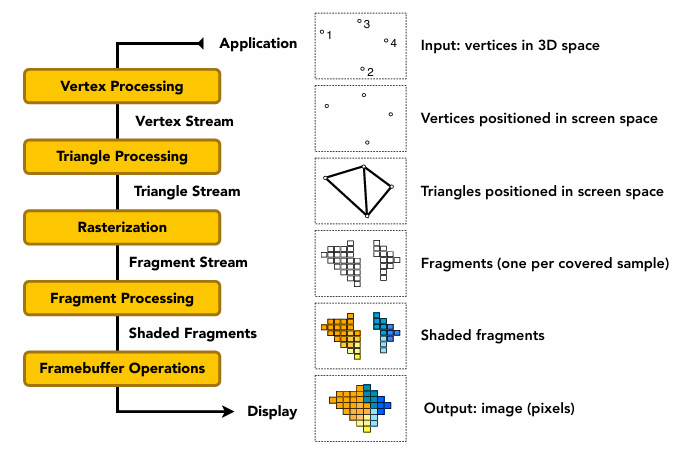
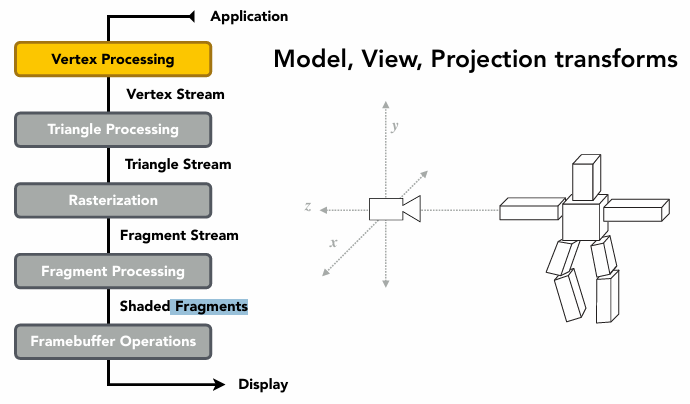
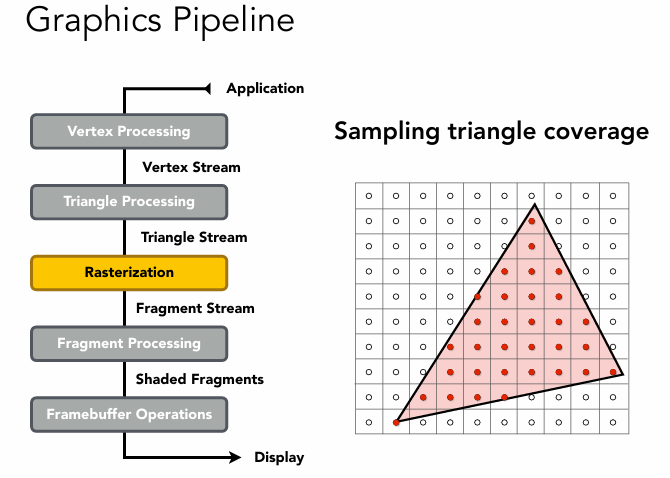
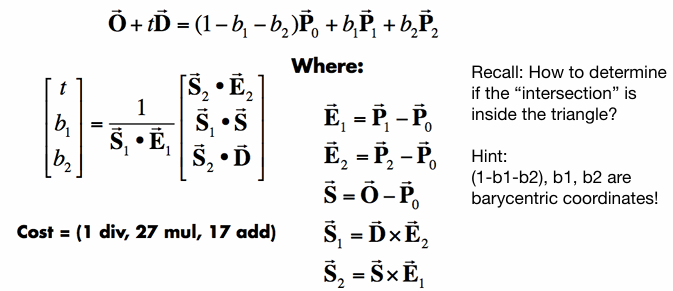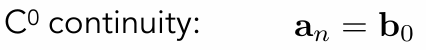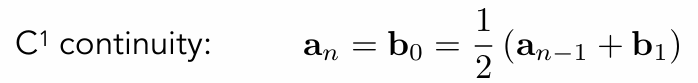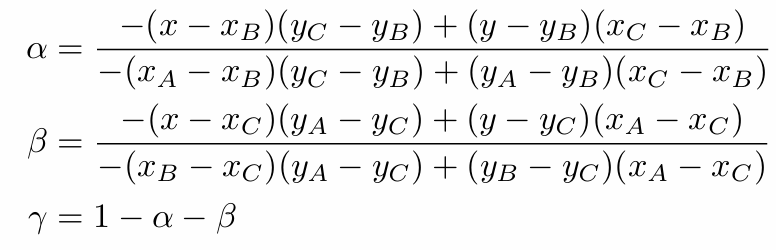Monte Carlo Integration
Why: we want to solve an integral, but it can be too difficult to solve analytically.
难以用解析法求解
数值解法:
1.黎曼积分:用很多小矩形近似
2.蒙特卡洛积分:多次采样近似

Example: Uniform Monte Carlo Estimator

Some notes:
• The more samples, the less variance.
• Sample on x, integrate on x.
Path Tracing
Motivation: Whitted-Style Ray Tracing
Whitted-style ray tracing:
-Always perform specular reflections / refractions
-Stop bouncing at diffuse surfaces
Are these simplifications reasonable?
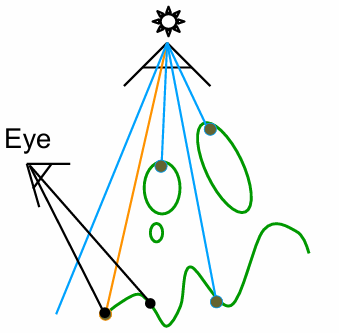
Whitted-Style Ray Tracing: Problem 1
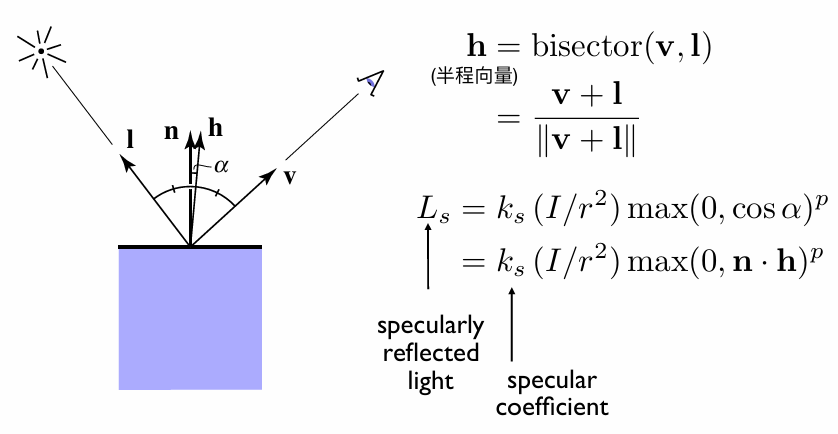
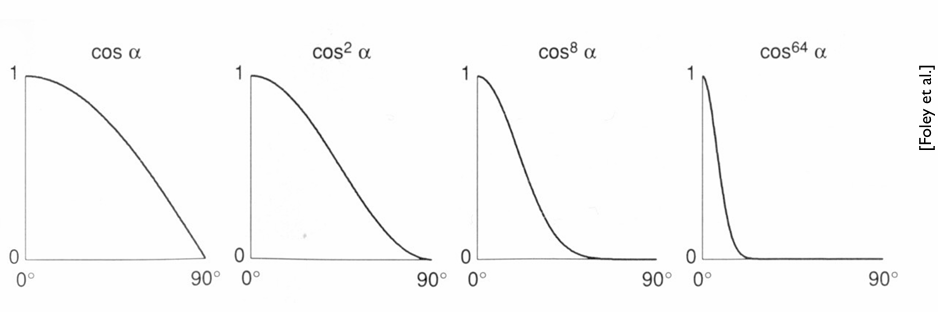
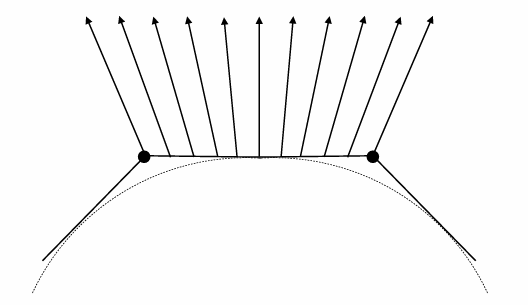
Where should the ray be reflected for glossy materials?

Whitted-Style Ray Tracing: Problem 2
No reflections between diffuse materials?
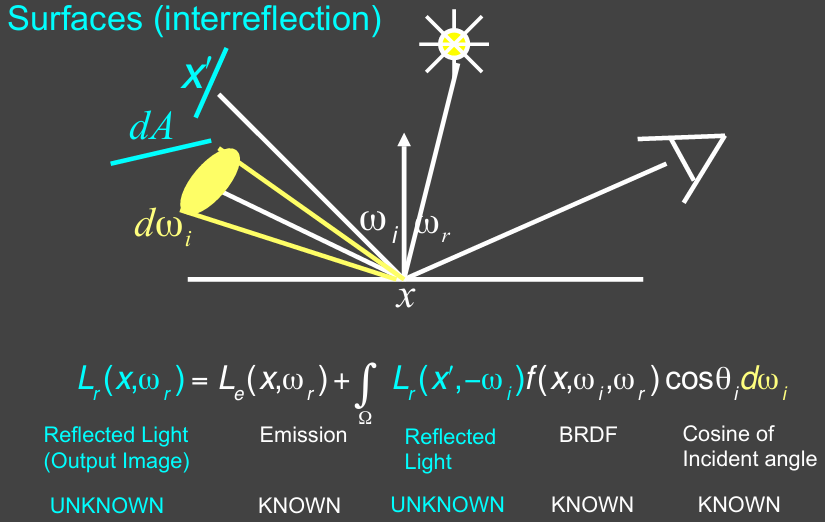
Whitted-Style Ray Tracing is Wrong
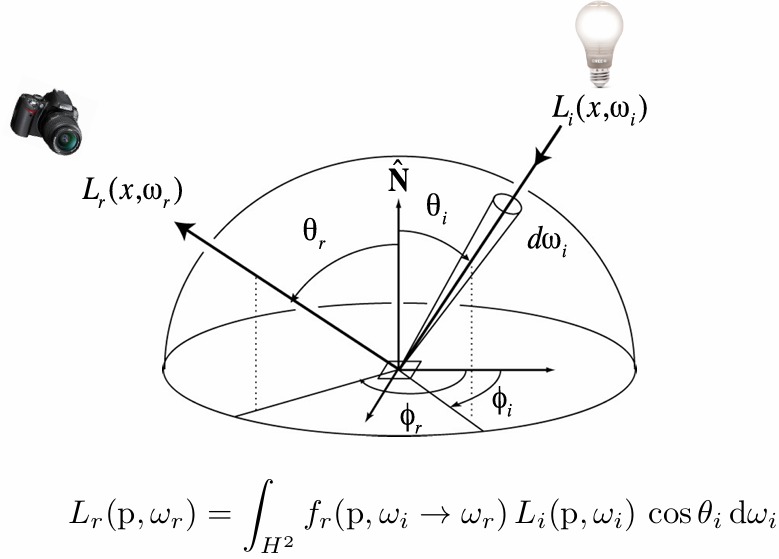
But the rendering equation is correct
But it involves
Solving an integral over the hemisphere, and
Recursive execution
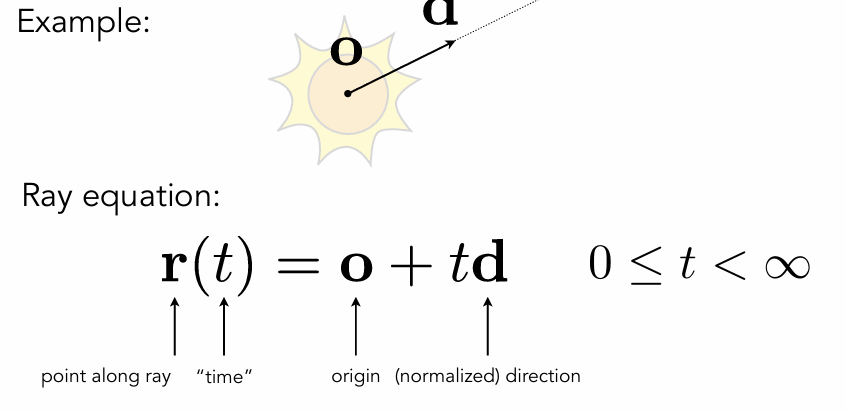
How do you solve an integral numerically?
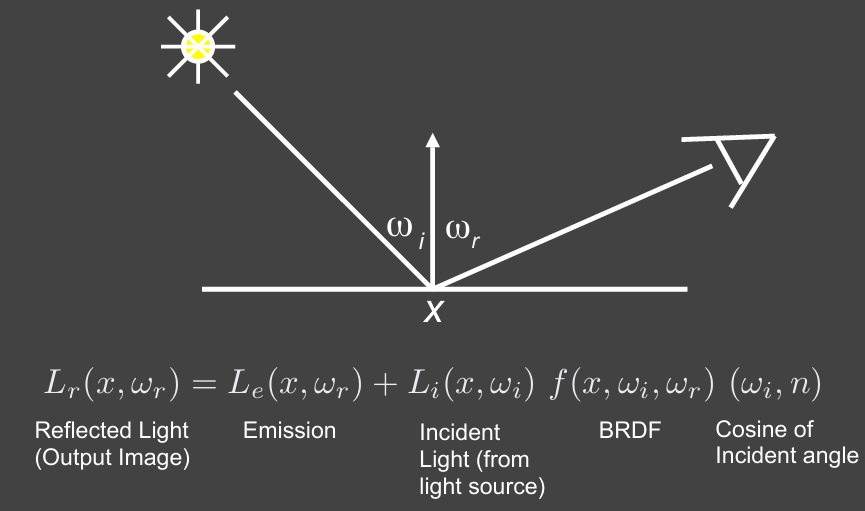
A Simple Monte Carlo Solution for direct illumination
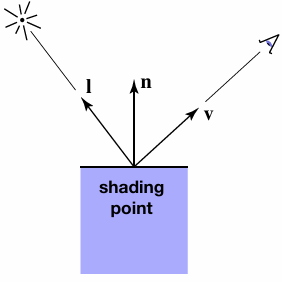
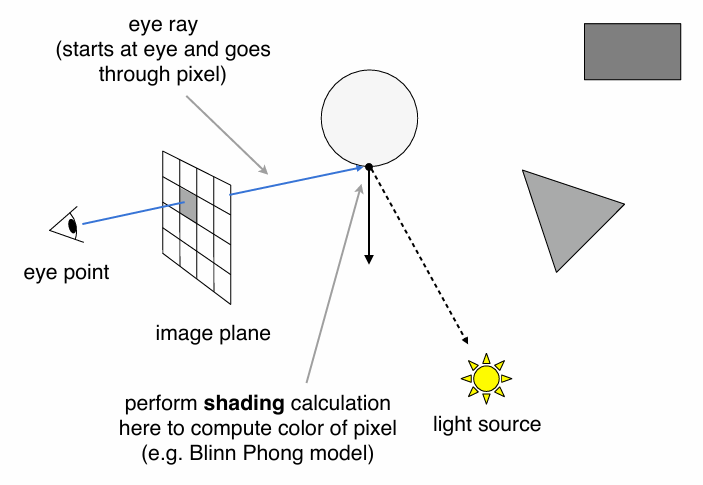
Suppose we want to render one pixel (point) in the following scene for direct illumination only
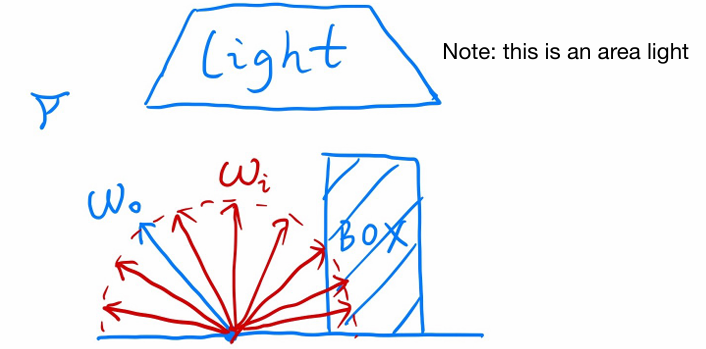
Abuse the concept of Reflection Equation a little bit
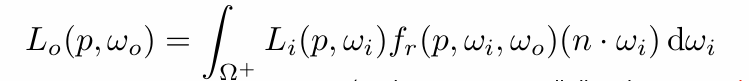
(assume all directions are pointing outwards)
Fancy as it is, it’s still just an integration over directions
So, of course we can solve it using Monte Carlo integration!

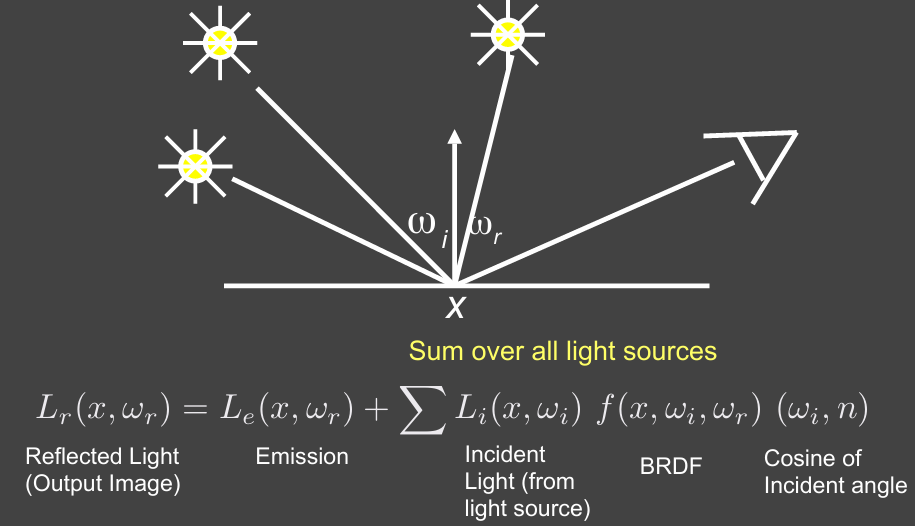
So, in general
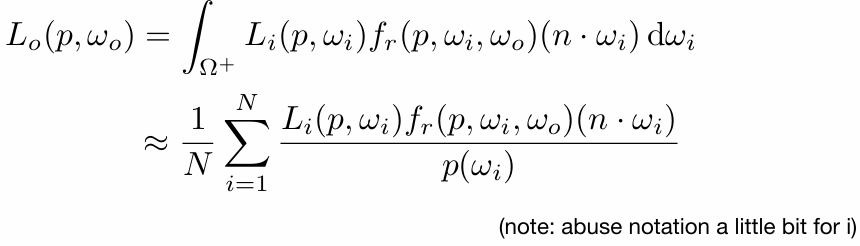
What does it mean?
A correct shading algorithm for direct illumination!
Code:

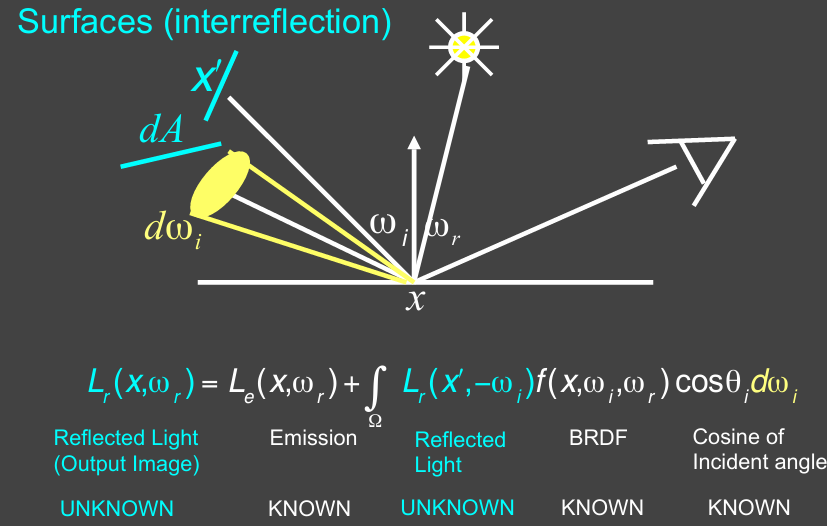
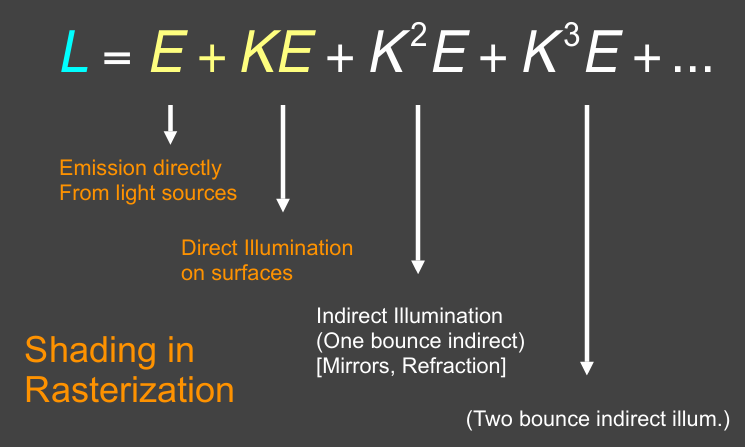
Introducing Global Illumination
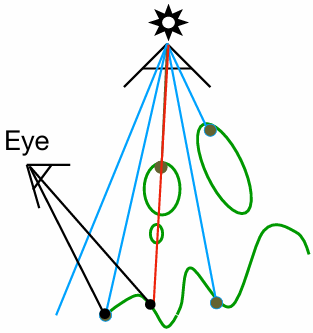
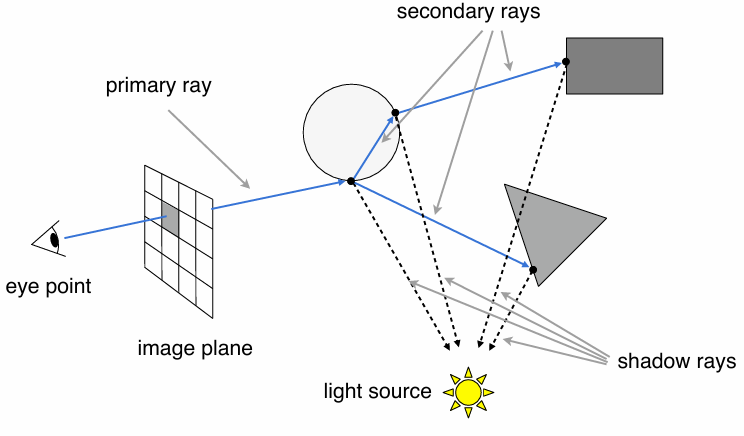
One more step forward: what if a ray hits an object?
Q also reflects light to P! How much? The dir. illum. at Q!
假设P点有个相机,计算Q点的直接光照
代码修改:

Problem 1: Explosion of #rays as #bounces go up:
#rays = N#bounces
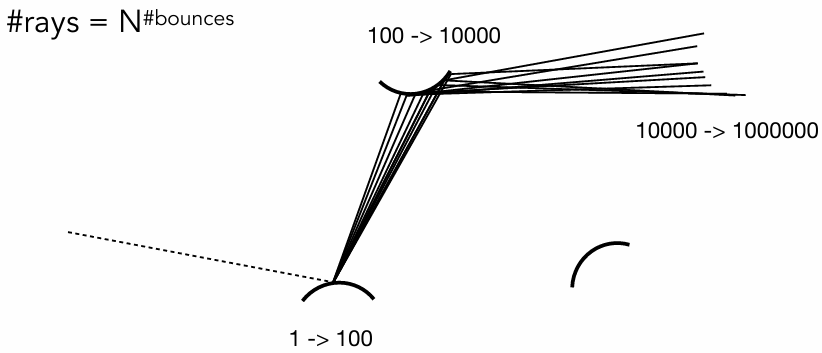
Key observation: #rays will not explode iff N = ???????
From now on, we always assume that only 1 ray is traced at each shading point:

This is path tracing! (FYI, Distributed Ray Tracing if N != 1)
But this will be noisy!
Ray Generation
No problem, just trace more paths through each pixel and average their radiance!
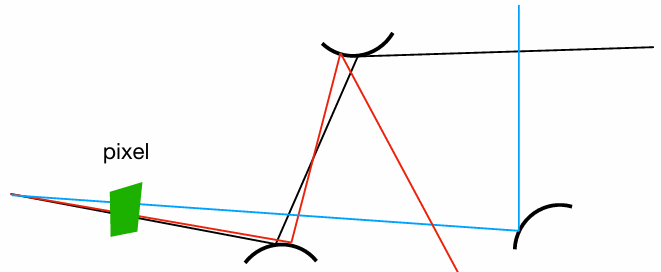
Very similar to ray casting in ray tracing

Problem 2: The recursive algorithm will never stop!
Dilemma: the light does not stop bouncing indeed!
Cutting #bounces == cutting energy!
Solution: Russian Roulette (RR) 俄罗斯轮盘赌
Russian Roulette is all about probability
With probability 0 < P < 1, you are fine
With probability 1 - P, otherwise

code:

Problem of sampling: low efficiency
Now we already have a correct version of path tracing!
But it’s not really efficient

(SPP the number of ray genetating at each pixel)
Sampling the Light
Understanding the reason of being inefficient
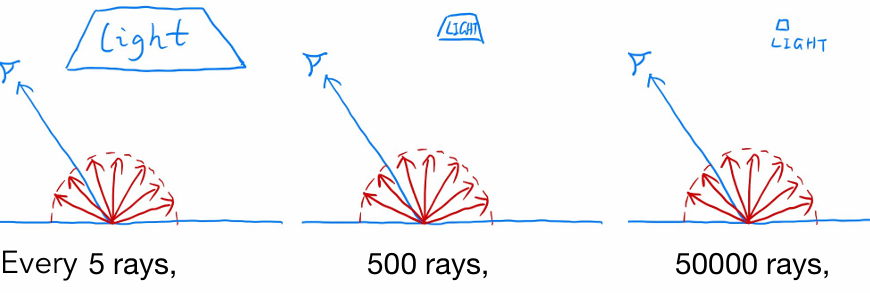
there will be 1 ray hitting the light. So a lot of rays are “wasted”if we uniformly sample the hemisphere at the shading point
想要在光源上采样,需要修改到在光源上积分。
Monte Carlo methods allows any sampling methods, so we can sample the light (therefore no rays are “wasted”)
Assume uniformly sampling on the light:
pdf = 1 / A (because ∫pdf dA = 1)
But the rendering equation integrates
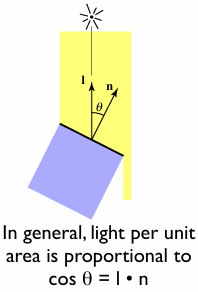
on the solid angle: Lo = ∫Li fr cos dω.
Recall Monte Carlo Integration:
Sample on x & integrate on x
Since we sample on the light, can we integrate on the light?
Need to make the rendering equation as an integral of dA
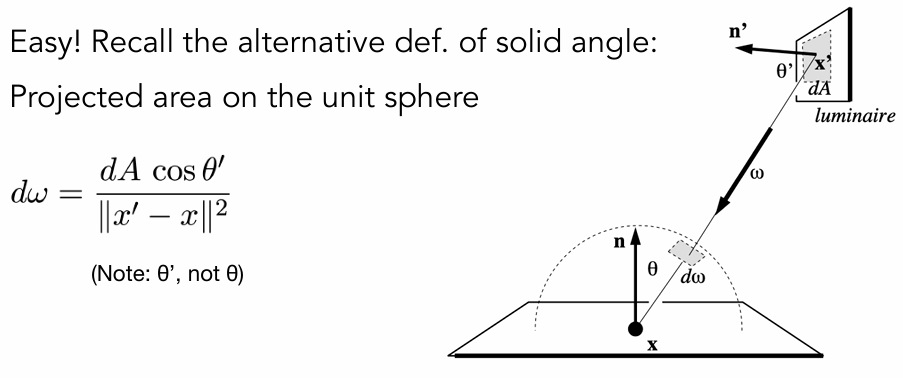
Need the relationship between dω and dA 寻找两者关系
Easy! Recall the alternative def. of solid angle:
Projected area on the unit sphere 投影到单位球面上
Then we can rewrite the rendering equation as
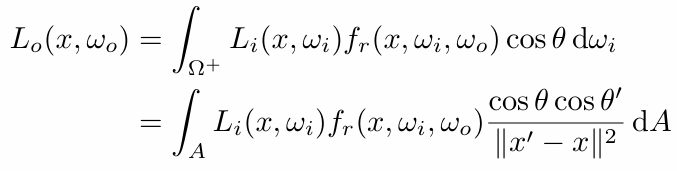
Now an integration on the light!
Monte Carlo integration:
“f(x)”: everything inside Pdf: 1 / A
Summary
Previously, we assume the light is “accidentally” shot by
uniform hemisphere sampling
分为2部分
Now we consider the radiance coming from two parts:
–light source (direct, no need to have RR) 直接来自光线,无需反射,即无需RR
–other reflectors (indirect, RR)
code:

One final thing: how do we know if the sample on the light is not blocked or not?
code:

Now path tracing is finally done!
点光源很难,可以做成很小的面积光源
Some Side Notes
• Path tracing (PT) is indeed difficult
-Consider it the most challenging in undergrad CS
-Why: physics, probability, calculus, coding
-Learning PT will help you understand deeper in these
• Is it still “Introductory”?
-Not really, but it’s “modern” :)
-And so learning it will be rewarding also because …
Ray tracing: Previous vs. Modern Concepts
• Previous
-Ray tracing == Whitted-style ray tracing
• Modern (the teacher’s definition)
-The general solution of light transport, including
-(Unidirectional & bidirectional) path tracing
-Photon mapping
-Metropolis light transport
-VCM / UPBP…
Things we haven’t covered / won’t cover
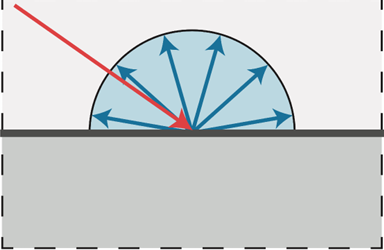
• Uniformly sampling the hemisphere
-How? And in general, how to sample any function? (sampling)
• Monte Carlo integration allows arbitrary pdfs
-What’s the best choice? (importance sampling)
• Do random numbers matter?
-Yes! (low discrepancy sequences)
• I can sample the hemisphere and the light
-Can I combine them? Yes! (multiple imp. sampling)
• The radiance of a pixel is the average of radiance on all paths passing through it
-Why? (pixel reconstruction filter)
• Is the radiance of a pixel the color of a pixel?
-No. (gamma correction, curves, color space)
• Asking again, is path tracing still “Introductory”?
-This time, yes. Fear the science, my friends
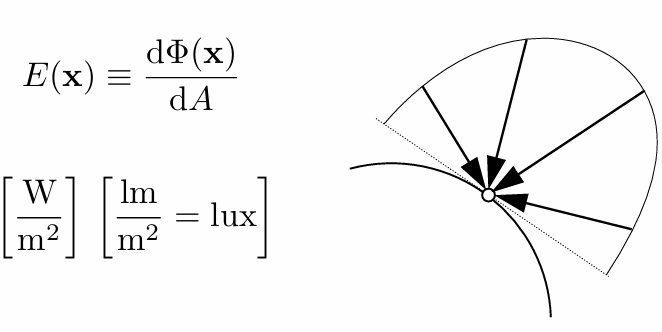
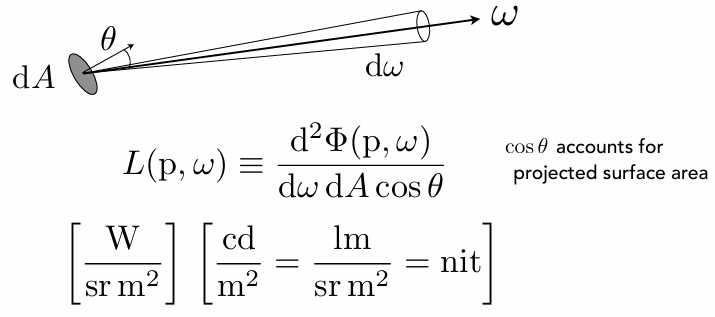
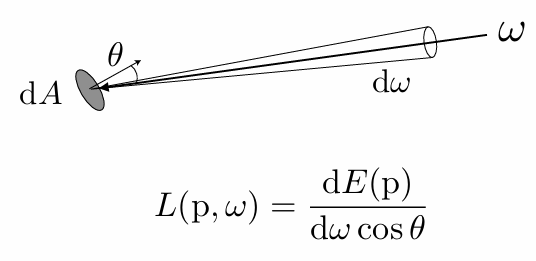


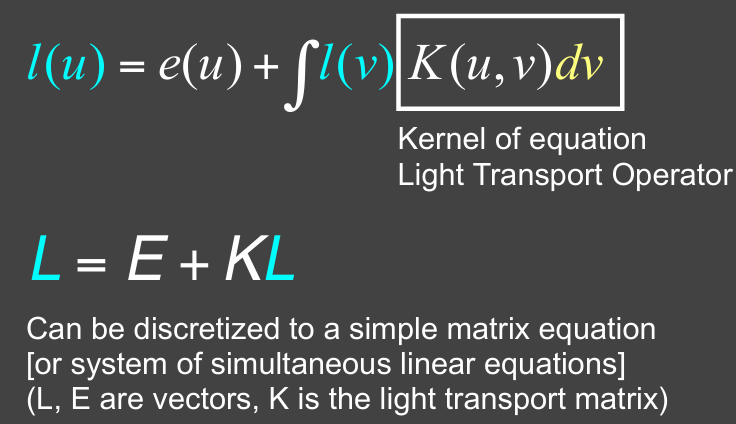

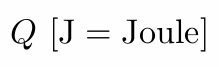
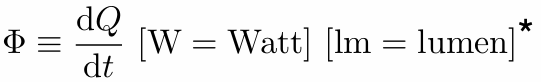
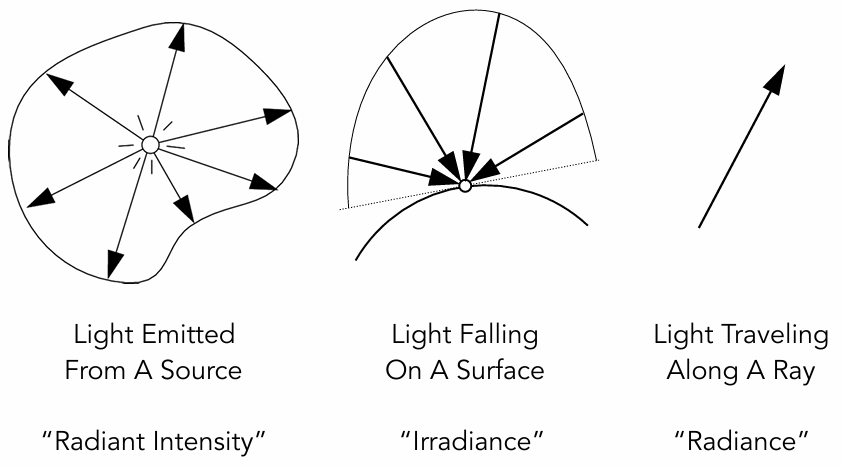
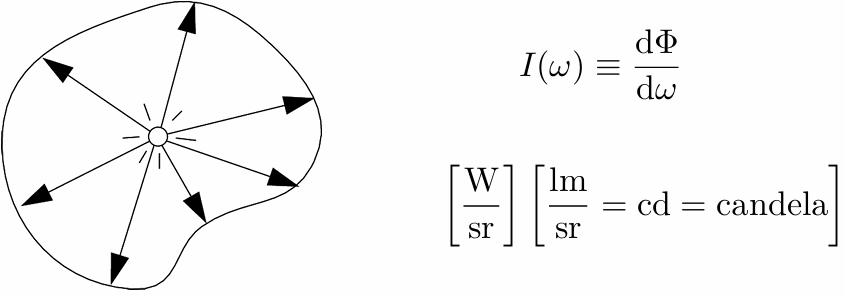

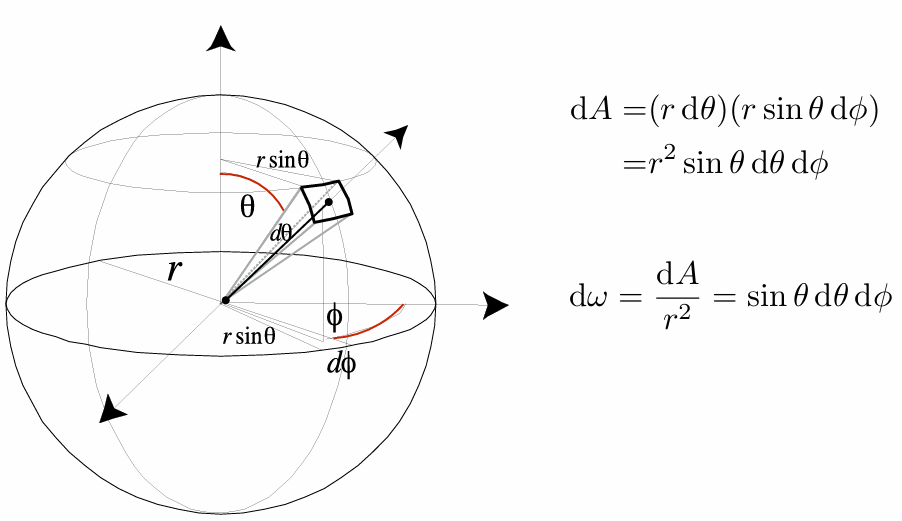
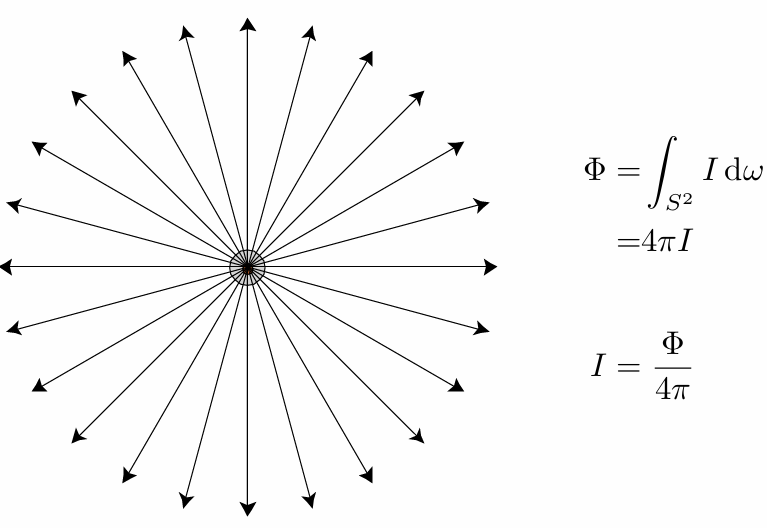
 、
、